 |
|
|||
Modelling the Educational Process in Asymmetric Information
Dumitru Marin
Daniela Marinescu
Table of Contents
Abstract
The level of education is highly related to the future possibilities to find a job. It is obvious that the people with university degrees have better chances that the other ones. A person with higher education degree has larger chances to go into the labour market and for a better position his well being will growth too. As well as the well being of people depending on him.
The Paper
The educational process is important not only for the main purpose to create an intelligent labour market capable to offer highly trained people to fulfil complex requests of modern world.
The signals offered by the labour force are due to the education received and reveal skills, wishes and other types of information that help the individual to evaluate himself for all his life. They also show information to a potential employer, information that help him to compare the abilities of a large number of individuals that wishes to be hired. The employer’s opinion about an individual just form knowing a certain signal is not perfect but their recognition is used instead of interviews, tests or training period.
If an individual passes a difficult exam (mathematics) with a high grade, the fact may represent a signal strong enough so an individual can work in IT where the information changes very fast.
The problem of educational signals is not recent; it represents the subject of many debates, especially since Michael Spence published his master thesis [5] in 1974. Previous papers belong to Arrow [1], Fields [2] and Thurov [7].
A complex educational signals is made by Stiglitz [6].
In the Principal-Agent model, there is a bidirectional relation between an institution (university, doctoral school, master, etc) and an individual (student, master student or PhD candidate) which has a contract as a result. The contract shows the demands and the rights of the two parties.
The individual (agent) makes an effort to obtain some results (passing exams, finishing research projects) and is rewarded for it.
In the situation of incomplete information (results can not be known for certain), X will be the set of possible results:
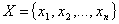
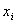 is a
possible result (a possible value of the income obtained by a research institution
from papers and studies publishing).
is a
possible result (a possible value of the income obtained by a research institution
from papers and studies publishing).
We shall consider a state where individual decisions are not based on exactly knowing the results of the individuals’ actions and not even on the utility of the results.
More possible results may be predicted together with different probabilities.
The probabilities can be objective or subjective.
The objective probabilities that don’t differ from one person to another represent the relative frequency of an even appearing.
The subjective or Bayesian probability shows the relative frequency by which an individual thinks that a certain event happens or differs from a person to another.
Frank Knight proposed the following classification scheme of the incomplete information problems:
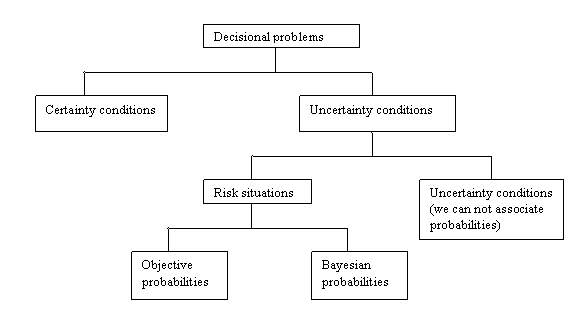
Both parties of the contract are risk averse or are indifferent to risk.
The attitude towards risk is characterized by a VNM utility function, both for the Agent and the Principal.
We assume that the necessary time needed by the Agent to produce a production unit
is
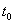 (before
the ending of the course) or the effort, production cost, etc.
(before
the ending of the course) or the effort, production cost, etc.
If the Agent wishes to go to a certain school, he must pay a sum of money S
(at the beginning) and then a sum of a for each monetary unit earned as a
consequence of the degree held by the Agent. Let t be the necessary time
to produce a unit or to earn a monetary unit after the graduation. Obviously, we
have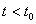
Next, we shall present a special type of contract adapted from [3, pg 149].
Definition1. A contract in symmetric information is given by the couple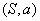
The market demand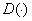
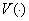 are expressed
as functions of average cost (or average time) denoted by x. If the price
of a unit produced is
are expressed
as functions of average cost (or average time) denoted by x. If the price
of a unit produced is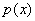
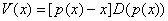 (1)
(1)
Proposition 1. If
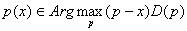
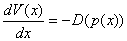
Proof
The derivative of
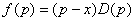 is
zero for
is
zero for
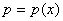
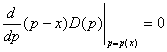
or
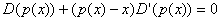 (2)
(2)
The revenue function from (1) derived with respect to x becomes:
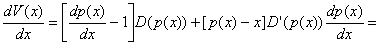
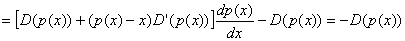
as in relation (2).
The Principal’s objective is to maximize the revenues and it can be written as:
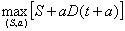
s.t.
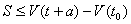 (3)
(3)
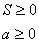
Theorem 1. The solution of the program (3) (the optimal contract under symmetric
information) is Pareto optimal and is given by the couple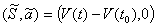
Proof
Using Kuhn-Tucker method, the multipliers
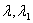 and
and
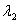 are
attached to the constraints in (3).
are
attached to the constraints in (3).
The Lagrangean function is:
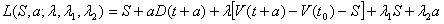
Searching for an interior optimum, we set the partial derivative with respect to S to zero:
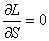 or
or
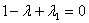
That is:
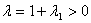
Then
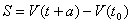 (the
first constraint is binding).
(the
first constraint is binding).
We can rewrite the program (3) in the following form:
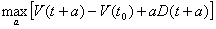
This provides us:
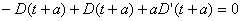
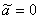 and
and
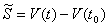
The partial derivatives of the Lagrangean function are:
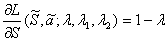
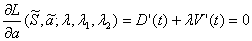
or
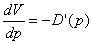 (4)
(4)
(4) corresponds to the condition for Pareto optimality satisfied by the optimal contract under symmetric information.
Next, we consider the same problem, but
in the case of asymmetric information, where the Agent has hidden information about
the contract. For instance, he knows how important is the production plan received
from the Decident. Further, we suppose that the type of the program is good (G)
- with probability
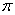 - or
bad - with the probability
- or
bad - with the probability
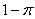
Definition2. A contract under asymmetric information is given by the couples:
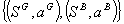
We have
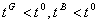 and
and
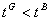
We can formulate now the Principal’s program (i.e., maximizing expected revenues):
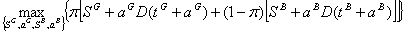
s.t.
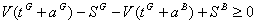 (5)
(5)
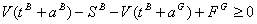 (6)
(6)
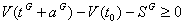 (7)
(7)
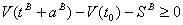 (8)
(8)
Theorem 2. The optimal contract under asymmetric information is characterized by:
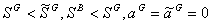 and
and
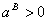
Proof
The Kuhn-Tucker multipliers
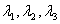 and
and
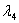
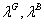
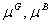 correspond to
correspond to 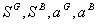 variables.
variables.
The restriction (7) is a consequence of the restrictions given by (5) and (8) (if the problem has admissible solution). To prove this, we have:
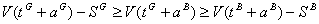
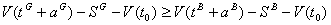
The Lagrangean function becomes:
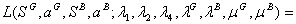
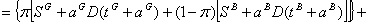
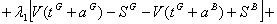
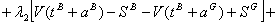
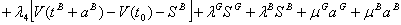
The first order conditions for an interior optimum are:
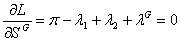 (9)
(9)
or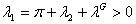
The first conclusion is that the restriction (5) is binding. Using this we find that:
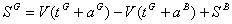 (10)
(10)
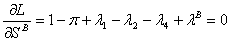 (11)
(11)
Adding the terms from (9) and (11), we obtain:
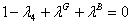 or
or
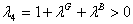
One result is that the restriction (8) is binding. Thus:
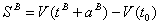 (12)
(12)
We shall use partial derivatives for the
Lagrangean function respected to the variables
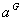 and
and
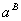 and
we have:
and
we have:
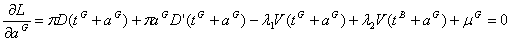
or
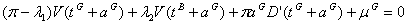
But
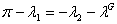 (from
(9)) and the precedent equation become:
(from
(9)) and the precedent equation become:
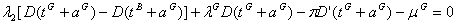 (12)
(12)
(12) shows that
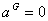 must
be stated.
must
be stated.
For
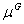
i)
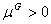
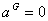
ii)
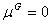
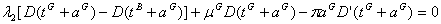
Because the variables’ coefficients
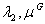 and
and
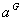 are
strictly positive, we have,
are
strictly positive, we have,
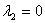 and
and
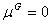
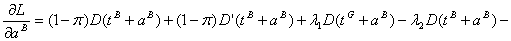
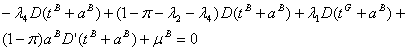
By conveniently combining the terms and
knowing that
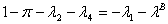
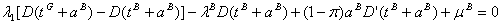
so that
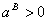
Obviously,
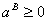
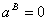
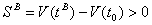 Because
Because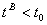
If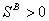
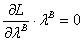 implies
implies
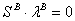 or
or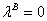
This is obtained from (13), because
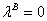
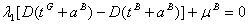 or
or
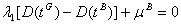
The first term is strictly positive, while
the second is negative. Thus,
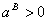
Finally, we can characterize the optimal contract.
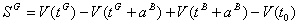
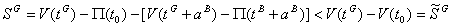
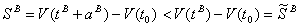
Using (10), we obtain:
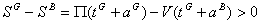
or
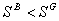
Thus, the optimal contract under asymmetric information is no longer Pareto optimal.
References
(top)
